離散一様分布の関数および特性値のまとめ
本ページでは,離散型確率変数 \( X \)の実現値\( k \)が,
\( k = 1,2,…,N \quad (ただし,Nは自然数) \)
\( k = a,…,b \quad (ただし,a,bはa < bの整数) \)
となるときの特性および関数の導出過程を掲載しています.
| 実現値 | \( k = 1,2,…,N \) \((ただし,Nは自然数) \) | \( k = a,a+1,…,b \) \((ただし,a,bはa < bの整数) \) |
| 確率質量関数(確率関数) \( f_X (k) \) | \( \dfrac{1}{N} \) | \( \dfrac{1}{b {}- a + 1} \) |
| 分布関数(累積分布関数) \( F_X (x) \) | \( \begin{cases} 0 & ( x < 1) \\ \dfrac{ \lfloor x \rfloor }{N} & (1 \leq x \leq N) \\ 1 & (x > N) \end{cases} \) | \( \begin{cases} 0 & ( x < a) \\ \dfrac{ \lfloor x \rfloor {}- a + 1}{b {}- a + 1} & (a \leq x \leq b) \\ 1 & (x > b) \end{cases} \) |
| 実現値 | \( k = 1,2,…,N \) \((ただし,Nは自然数) \) | \( k = a,a+1,…,b \) \((ただし,a,bはa < bの整数) \) |
| 期待値 \( E[x] \) | \( \dfrac{N + 1}{2} \) | \( \dfrac{a + b}{2} \) |
| 分散 \( Var[x] \) | \( \dfrac{N^{2} {}- 1}{12} \) | \( \dfrac {(b {}- a + 1)^{2} {}- 1}{12} \) |
\( k = 1,2,…,N \)のとき
確率質量関数(確率関数)
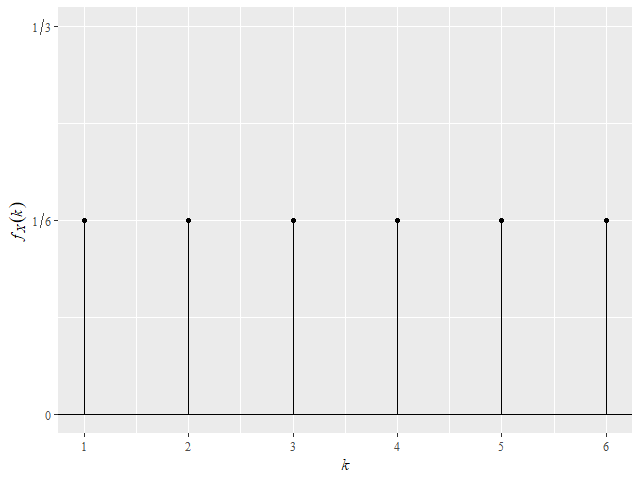
離散型確率変数\( X \)が離散一様分布に従うとき、その確率質量関数(確率関数)は以下である。
\begin{eqnarray*}
f_X (k) & = & P(X = k) \\
& = & \dfrac{1}{N} \quad (k = 1, 2, …, N)
\end{eqnarray*}
\( k : 実現値 \)
\( N : 自然数 \)
\( m \)から\( n \)(ただし、\( m, n \)は\( m < n \)の整数)までの整数の個数を求める公式
\begin{eqnarray*}
整数の個数 & = & n {}- m + 1 \\
& = & N {}- 1 + 1 \\
& = & N
\end{eqnarray*}
離散型確率変数\( X \)が離散一様分布に従うとき、実現値\( k \)を同じ確率でとる。
分布関数(累積分布関数)
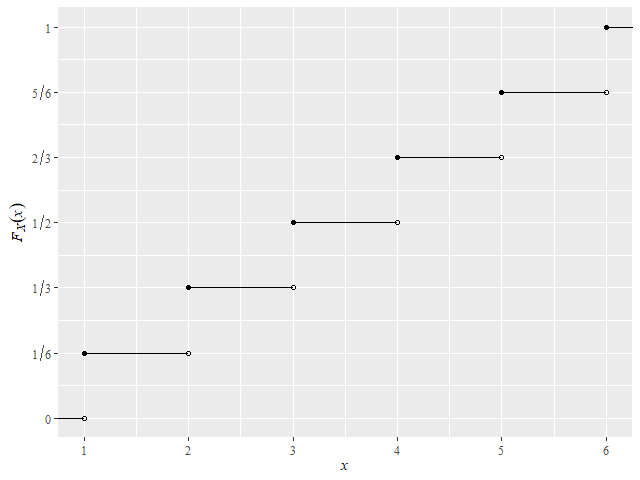
分布関数(累積分布関数)は、すべての実数\( x \)に対して以下のように定義される(※離散確率変数\( X \)の実現値\( k \)に対して定義されるわけではない)。
\begin{eqnarray*}
F_X (x) & = & P(X \leq x) \\
& = &
\begin{cases}
0 & ( x < 1) \\
\dfrac{ \lfloor x \rfloor }{N} & (1 \leq x \leq N) \\
1 & (x > N)
\end{cases}
\end{eqnarray*}
※\( \lfloor x \rfloor \)は、「\( x \)を超えない最大の整数」である。\( \lfloor x \rfloor \)は\( [x] \)と表されることもあり、このとき\( [ \quad ] \)はガウス記号と呼ばれる。
確率母関数
\begin{eqnarray*}
G_X (s) & = & E [ s^X] \\
& = & \sum_{k = 0}^{ \infty} s^k P(X = k) \\
ここで、 \\
P(X = k) & = &
\begin{cases}
0 & ( k \notin \{ 1,2,…,N \} ) \\
\dfrac{1}{N} & ( k \in \{ 1,2,…,N \} ) \\
\end{cases} \\
であるから、 \\
G_X (s) & = & \sum_{k = 0}^{ \infty} s^k P(X = k) \\
& = & \sum_{k = 1}^{ N} s^k P(X = k) \\
& = & \dfrac{1}{N} \displaystyle \sum_{k = 1}^{N} s^k
\end{eqnarray*}
積率母関数(モーメント母関数)
\begin{eqnarray*}
M_X (t) & = & E \left [ e^{tX} \right ] \\
& = & \displaystyle \sum_{k = 1}^{N} e^{tk}P(X = k) \\
& = & \dfrac{1}{N} \sum_{k = 1}^{N} (e^{t})^{k} \\
& = & \dfrac{e^{t}}{N} \sum_{k = 1}^{N} (e^{t})^{k {}- 1} \\
& = & \dfrac{e^{t}}{N} \dfrac{1 {}- e^{tN}}{1 {}- e^{t}} \\
& = & \dfrac{e^{t} \left( 1 {}- e^{tN} \right)}{N\left( 1 {}- e^{t} \right)}
\end{eqnarray*}
期待値(平均)
\begin{eqnarray*}
E[X] & = & \displaystyle \sum_{k = 1}^{N} k f_X(k) \\
& = & \displaystyle \sum_{k = 1}^{N} kP(X = k) \\
& = & \dfrac{1}{N} \displaystyle \sum_{k = 1}^{N} k \qquad (確率質量関数の式より) \\
& = & \dfrac{1}{N} \dfrac{N(N + 1)}{2} \qquad(シグマ公式より) \\
& = & \dfrac{N + 1}{2}
\end{eqnarray*}
(例) サイコロの出目\( (x = 1,2,…,6) \)の期待値は、
\( E[X] = \dfrac{6 + 1}{2} = 3.5 \)
分散
\begin{eqnarray*}
Var(X) & = & E[(X {}- \mu)^{2}] \\
& = & E[X^{2} {}- 2 \mu X + \mu^{2}] \\
& = & E[X^{2}] {}- 2\mu E[X] + \mu^{2} \\
& = & E[X^{2}] {}- 2E[X]E[X] + \{ E[X] \}^{2} \qquad ( \mu = E[X]より) \\
& = & E[X^{2}] {}- \{ E[X] \}^{2} \\
ここで、\\
E[X^{2}] & = & \displaystyle \sum_{k = 1}^{N} k^{2} P(X = k) \\
&=& \dfrac{1}{N} \displaystyle \sum_{k = 1}^{N} k^{2} \qquad (確率質量関数の式より) \\
&=& \dfrac{1}{N} \dfrac {N(N + 1)(2N + 1)}{6} \qquad (シグマ公式より) \\
&=& \dfrac{(N + 1)(2N + 1)}{6} \\
より、 \\
Var(X) & = & E[X^{2}] {}- \{ E[X] \} ^{2} \\
&=& \dfrac{(N + 1)(2N + 1)}{6} {}- \left \{ \dfrac{N + 1}{2} \right \} ^{2} \\
&=& \dfrac{N^{2} {}- 1}{12}
\end{eqnarray*}
シグマ公式
\( \displaystyle \sum_{k = 1}^{N} k^{2} = \dfrac {N(N + 1)(2N + 1)}{6} \)
(例) サイコロの出目\( (x = 1,2,…,6) \)の分散は、
\( Var(X) = \dfrac{(6 + 1)(6 {}- 1)}{12} = 2.9166… \)
\( k = a,a+1,…,b \) のとき
確率質量関数(確率関数)
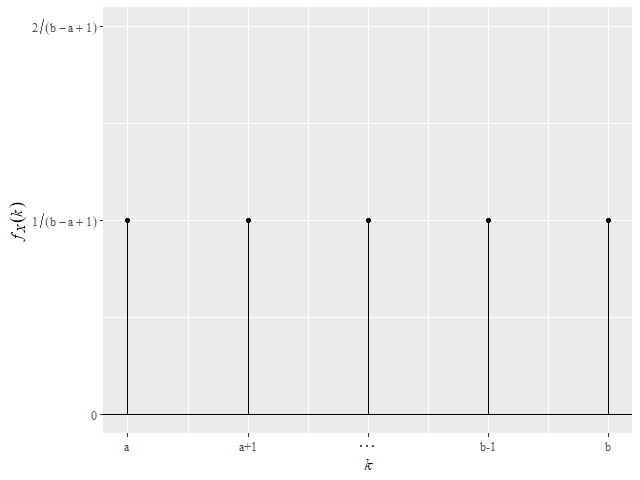
離散型確率変数\( X \)が離散一様分布に従うとき、その確率質量関数(確率関数)は以下である。
\begin{eqnarray*}
f_X (k) & = & P(X = k) \\
& = & \dfrac{1}{b {}- a + 1} \quad (k = a, a + 1, …, b)
\end{eqnarray*}
\( k:実現値 \)
\( N:自然数 \)
\( m \)から\( n \)(ただし、\( m, n \)は\( m < n \)の整数)までの整数の個数を求める公式
\begin{eqnarray*}
整数の個数 & = & n {}- m + 1 \\
& = & b {}- a + 1 \\
\end{eqnarray*}
離散型確率変数Xが離散一様分布に従うとき、実現値\( k \)を同じ確率でとる。
分布関数(累積分布関数)
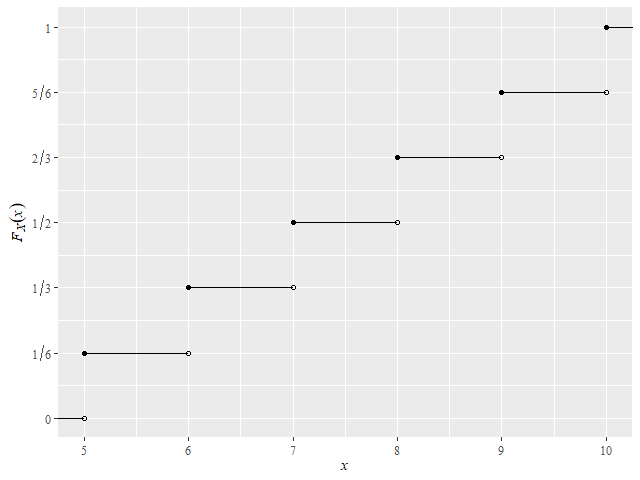
分布関数(累積分布関数)は、すべての実数\( x \)に対して以下のように定義される(※離散確率変数\( X \)の実現値\( k \)に対して定義されるわけではない)。
\begin{eqnarray*}
F_X (x) & = & P(X \leq x) \\
& = &
\begin{cases}
0 & ( x < a) \\
\dfrac{ \lfloor x \rfloor {}- a + 1}{b {}- a + 1} & (a \leq x \leq b) \\
1 & (x > b)
\end{cases}
\end{eqnarray*}
※\( \lfloor x \rfloor \)は、「\( x \)を超えない最大の整数」である。\( \lfloor x \rfloor \)は\( [x] \)と表されることもあり、このとき\( [ \quad ] \)はガウス記号と呼ばれる。
積率母関数(モーメント母関数)
\begin{eqnarray*}
M_X (t) & = & E \left [ e^{tX} \right ] \\
& = & \displaystyle \sum_{k = a}^{b} e^{tk}P(X = k) \\
& = & \dfrac{1}{b {}- a + 1} \sum_{k = a}^{b} (e^{t})^{k} \\
& = & \dfrac{1}{b {}- a + 1} \sum_{k = 1}^{b {}- a + 1} (e^{t})^{k + a{}- 1} \\
& = & \dfrac{(e^{t})^{a}}{b {}- a + 1} \sum_{k = 1}^{b {}- a + 1} (e^{t})^{k {}- 1} \\
& = & \dfrac{e^{at}}{b {}- a + 1} \dfrac{1 {}- (e^{t})^{b {}- a + 1}}{1 {}- e^{t}} \\
& = & \dfrac{e^{at} -e^{(b + 1)t}}{\left( b {}- a + 1 \right) \left( 1 {}- e^{t} \right)}
\end{eqnarray*}
期待値(平均)
\begin{eqnarray*}
E[X] & = & \displaystyle \sum_{k = a}^{b} k f_X(k) \\
& = & \displaystyle \sum_{k = a}^{b} k P(X = k) \\
& = & \dfrac{1}{b {}- a + 1} \displaystyle \sum_{k = a}^{b} k \qquad (確率質量関数の式より) \\
& = & \dfrac{1}{b {}- a + 1} \dfrac{(b {}- a + 1)(a+ b)}{2} \qquad(シグマ公式より) \\
& = & \dfrac{a + b}{2}
\end{eqnarray*}
(例) サイコロの出目\( (x = 1,2,…,6) \)の期待値は、
\( E[X] = \dfrac{6 + 1}{2} = 3.5 \)
分散
\begin{eqnarray*}
Var(X) & = & E[(X {}- \mu)^{2}] \\
& = & E[X^{2} {}- 2 \mu X + \mu^{2}] \\
& = & E[X^{2}] {}- 2\mu E[X] + \mu^{2} \\
& = & E[X^{2}] {}- 2E[X]E[X] + \{ E[X] \}^{2} \qquad ( \mu = E[X]より) \\
& = & E[X^{2}] {}- \{ E[X] \}^{2} \\
ここで、\\
E[X^{2}] & = & \displaystyle \sum_{k = a}^{b} k^{2} f_X (k) \\
& = & \displaystyle \sum_{k = a}^{b} k^{2} P(X = k) \\
& = & \dfrac{1}{b {}- a + 1} \displaystyle \sum_{k = a}^{b} k^{2} \qquad (確率質量関数の式より) \\
& = & \dfrac{1}{b {}- a + 1} \displaystyle \sum_{k = 1}^{b {}- a + 1} (k + a {}- 1)^{2} \\
& = & \dfrac{1}{b {}- a + 1} \displaystyle \sum_{k = 1}^{b {}- a + 1} \{k^{2} + 2(a {}- 1)k + (a {}- 1)^{2} \} \\
& = & \dfrac{1}{b {}- a + 1} \left [ \dfrac {(b {}- a + 1)(b {}- a + 2) \{ 2(b {}- a + 1) + 1 \} }{6} + \dfrac{2(a {}- 1)(b {}- a + 1)(b {}- a + 2)}{2} + (b {}- a + 1)(a {}- 1)^{2} \right ] \qquad (シグマ公式より) \\
& = & \dfrac {(b {}- a + 2) \{ 2(b {}- a + 1) + 1 \} }{6} + (a {}- 1)(b {}- a + 2) +(a {}- 1)^{2} \\
& = & \dfrac {2a^{2} + 2b^{2} {}- 4ab {}- 7a + 7b + 6}{6} + ab + a {}- b {}- 1\\
& = & \dfrac {2a^{2} + 2b^{2} {}- 4ab {}- 7a + 7b + 6}{6} + \dfrac {6ab + 6a {}- 6b {}- 6}{6} \\
& = & \dfrac {2a^{2} + 2b^{2} + 2ab {}- a + b}{6} \\
より、 \\
Var(X) & = & E[X^{2}] {}- \{ E[X] \} ^{2} \\
& = & \dfrac {2a^{2} + 2b^{2} + 2ab {}- a + b}{6} {}- \left \{ \dfrac{a + b}{2} \right \}^{2} \\
& = & \dfrac {4a^{2} + 4b^{2} + 4ab {}- 2a + 2b}{12} {}- \dfrac{3a^{2} + 6ab + 3b^{2}}{12} \\
& = & \dfrac {a^{2} + b^{2} {}- 2ab {}- 2a + 2b}{12} \\
& = & \dfrac {b^{2} {}- 2ab + a^{2} + 2b {}- 2a}{12} \\
& = & \dfrac {(b {}- a)^{2} + 2(b {}- a)}{12} \\
& = & \dfrac {(b {}- a)^{2} + 2(b {}- a) + 1 {}- 1}{12} \\
& = & \dfrac {(b {}- a + 1)^{2} {}- 1}{12}
\end{eqnarray*}
(例) サイコロの出目\( (x = 1,2,…,6) \)の分散は、
\( Var(X) = \dfrac{(6 + 1)(6 {}- 1)}{12} = 2.9166… \)
